Interacción Débil

La interacción débil es una de las fuerzas fundamentales de la naturaleza, junto con la fuerte, la electromagnética y la gravitatoria. Actúa tanto sobre leptones (como electrones y neutrinos) como sobre quarks, y se manifiesta mediante el intercambio de bosones mediadores: $W^+$, $W^-$ y $Z^0$. A menudo se la conoce también como la carga débil.

Es la única fuerza capaz de modificar el sabor de las partículas elementales, transformando un quark o un leptón en otro de la misma familia.

Gracias a esta propiedad, es responsable de procesos como la desintegración beta en núcleos inestables. Y dado que los neutrinos se producen y se detectan a través de interacciones débiles en sus estados de sabor, esta fuerza está también estrechamente vinculada al fenómeno de las oscilaciones de neutrinos.

Su alcance es extremadamente corto (del orden de $10^{-18}$ m), y su intensidad es mucho menor que la de la fuerza fuerte o la electromagnética. A bajas energías puede ser hasta $10^{11}$ veces más débil que el electromagnetismo.

Es importante aclarar que los valores citados para la intensidad relativa de las fuerzas son solo aproximaciones a bajas energías. En realidad, las constantes de acoplamiento varían con la escala de energía del proceso. En líneas generales, la interacción débil es entre $10^{5}$ y $10^{13}$ veces más débil que la fuerza fuerte.

Nota. A pesar de su debilidad, la interacción débil cumple un papel esencial tanto en la física de partículas como en la astrofísica: por ejemplo, en las reacciones nucleares que hacen brillar a las estrellas.

La Desintegración Beta y la Interacción Débil

La interacción débil es la base de la desintegración beta, un proceso radiactivo que permite a un núcleo atómico inestable transformarse en otro más estable.

Un núcleo resulta inestable cuando presenta una relación desequilibrada entre neutrones y protones.

La desintegración beta corrige ese desequilibrio convirtiendo un neutrón en un protón, o viceversa. Es una de las formas principales de radiactividad natural, junto con las desintegraciones alfa y gamma.

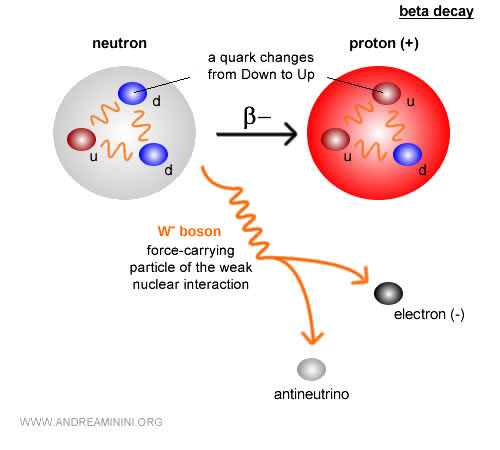
• Desintegración beta (β⁻)
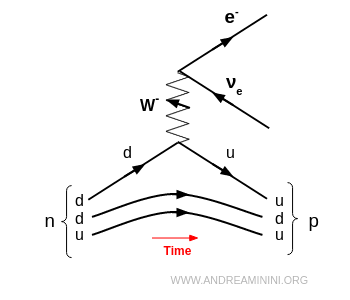
  Un neutrón se transforma en un protón, emitiendo un electrón y un antineutrino electrónico: $$ n \;\;\to\;\; p + e^- + \bar{\nu}_e $$ A nivel de quarks, un quark down se convierte en un quark up al emitir un bosón virtual \$W^-\$, que se desintegra casi de inmediato en \$e^-\$ y \$\bar{\nu}\_e\$.
  
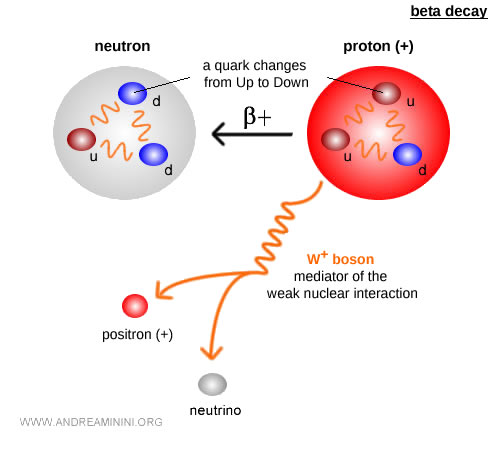
• Desintegración beta (β⁺)
  Un protón se convierte en un neutrón, emitiendo un positrón y un neutrino electrónico: $$p \;\;\to\;\; n + e^+ + \nu_e$$ Aquí, un quark up se transforma en un quark down al emitir un bosón virtual \$W^+\$, que luego se desintegra en \$e^+\$ y \$\nu\_e\$.
  

  

Este mecanismo permite al núcleo ajustar su proporción de neutrones y protones, alcanzando una configuración más estable en términos de energía.

Además de ser una de las fuentes naturales de radiactividad, la desintegración beta tiene un papel fundamental en las reacciones nucleares que alimentan a las estrellas, incluido el Sol.

Modalidades de la Interacción Débil: Neutra y Cargada

La interacción débil se presenta en dos formas distintas.

• Interacciones débiles neutras (NC, Neutral Current)
  Están mediadas por bosones $Z$. En estos procesos, el fermión que entra en el vértice es el mismo que sale: no hay cambio de sabor, igual que en las interacciones electromagnéticas o fuertes. Lo que las distingue es su violación de la paridad, una huella característica que permite detectarlas incluso cuando se manifiestan de manera sutil en procesos dominados por el electromagnetismo, como en ciertos experimentos de física atómica.

  Nota. Las interacciones cargadas se identificaron ya en los años treinta gracias al trabajo pionero de Fermi sobre la desintegración beta. Las interacciones neutras, en cambio, fueron predichas recién a finales de los sesenta por Glashow, Weinberg y Salam dentro de la teoría electrodébil (GWS). Su existencia se confirmó de forma espectacular en el CERN en 1973, un hito en la física de partículas: hasta entonces solo se conocían procesos mediados por bosones $W$; el descubrimiento de las corrientes neutras fue una auténtica revolución.

• Interacciones débiles cargadas (CC, Charged Current)
  Están mediadas por bosones $W$. A diferencia de cualquier otra fuerza fundamental, pueden cambiar el sabor de las partículas. Así, un quark up puede transformarse en un quark down, o un electrón en un neutrino electrónico. Esta capacidad de modificar el sabor convierte a las interacciones cargadas en el auténtico motor de los procesos de desintegración, como la desintegración beta nuclear.

  Nota. En la interacción fuerte, los quarks pueden cambiar de color (por ejemplo, de rojo a verde) pero no de sabor; en las interacciones electromagnéticas, los fermiones (quarks y leptones) pueden emitir o absorber fotones sin alterar ni sabor ni carga. Lo mismo ocurre en las interacciones débiles neutras (NC), mediadas por el bosón $Z$. En cambio, en las interacciones débiles cargadas (CC), mediadas por los bosones $W^\pm$, una partícula sí puede cambiar de sabor: por ejemplo, un quark up puede convertirse en un quark down, lo que permite que un protón se transforme en un neutrón, o al revés.

Antes de ver ejemplos concretos, la siguiente tabla resume de un vistazo las diferencias esenciales entre las interacciones débiles neutras y cargadas.

Tipo de interacción	Mediador	Cambio de sabor	Característica distintiva
Débil neutra (NC)	Bosón Z0	No	Viola la paridad, pero conserva la carga y la identidad de la partícula
Débil cargada (CC)	Bosones W±	Sí	Impulsa procesos de desintegración, transformando un fermión en otro

Ejemplos Prácticos

Algunos ejemplos clásicos de interacción débil son la dispersión neutrino-electrón $ \nu_{\mu} + e^- \to \nu_{\mu} + e^- $ y la dispersión neutrino-protón $ \nu_{\mu} + p \to \nu_{\mu} + p $.

Dispersión neutrino-electrón

En este proceso, un neutrino ($\nu$) choca con un electrón ($e^-$), desviándolo y transfiriéndole parte de su energía y momento: $$ \nu + e^- \;\to\; \nu + e^- $$ Se trata de un fenómeno extremadamente raro, ya que los neutrinos carecen de carga eléctrica y no interactúan mediante el electromagnetismo. La interacción débil es el único canal posible.

Existen dos mecanismos distintos:

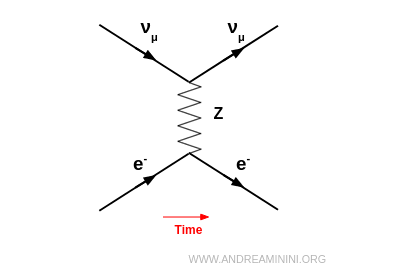
• Dispersión por corriente neutra (mediada por $Z^0$)
  Puede darse con todos los sabores de neutrinos ($\nu_e, \nu_\mu, \nu_\tau$). El neutrino intercambia un bosón virtual $Z^0$ con el electrón y sale con el mismo sabor: $$ \nu_\mu + e^- \;\to\; \nu_\mu + e^- $$ Solo varían su energía y dirección, por lo que la colisión es elástica.
  
• Dispersión por corriente cargada (mediada por $W^\pm$)
  En este caso, un neutrino electrónico $\nu_e$ se convierte en un electrón al intercambiar un bosón $W$ con el electrón objetivo, que pasa a ser un neutrino electrónico: $$ \nu_e + e^- \;\to\; e^- + \nu_e $$ En la práctica, neutrino y electrón intercambian identidades. El resultado final se asemeja al de la dispersión neutra, aunque aquí el mediador es un $W$ en lugar de un $Z$.

Nota. La dispersión neutrino-electrón fue uno de los primeros procesos que confirmaron la existencia de corrientes débiles neutras en el CERN en 1973. Se la considera una prueba “limpia”, ya que no intervienen nucleones ni la interacción fuerte, lo que permite contrastar directamente la teoría electrodébil.

Dispersión neutrino-protón

En la dispersión neutrino-protón, un neutrino interactúa directamente con un protón.

Como los neutrinos no tienen carga eléctrica y no sienten la interacción fuerte, los únicos mediadores posibles son los bosones débiles $W^\pm$ y $Z^0$.

Al igual que en el caso neutrino-electrón, existen dos modalidades principales:

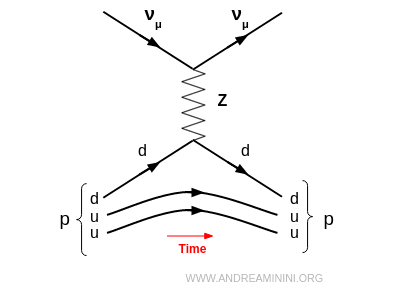
• Dispersión por corriente neutra (NC)
  Mediado por el bosón $Z^0$. El neutrino conserva su sabor y el protón no cambia de identidad. Solo se redistribuyen energía y momento (dispersión elástica). Por ejemplo, un neutrino muónico dispersándose en un protón: $$ \nu_\mu + p \;\to\; \nu_\mu + p $$ Esta reacción fue decisiva en el descubrimiento de las corrientes neutras en el CERN en 1973.
  
• Dispersión por corriente cargada (CC)
  Mediado por el bosón $W^\pm$. El neutrino se convierte en un leptón cargado, mientras que el protón se transforma en otro nucleón (protón ↔ neutrón). Por ejemplo, cuando un neutrino electrónico interactúa con un protón, produce un positrón y convierte el protón en un neutrón: $$ \nu_e + p \;\to\; e^+ + n $$ Este proceso es, en esencia, el inverso de la desintegración beta.

Ambos tipos de dispersión son extremadamente infrecuentes. Para detectarlos se necesitan instalaciones de gran tamaño y haces de neutrinos muy intensos.

Interacción Débil entre Leptones

La interacción débil cargada entre leptones, mediada por los bosones $W^\pm$, permite que un neutrino (carga $0$) y su leptón cargado asociado (carga $-e$) se transformen mutuamente, pero siempre dentro de la misma generación.

La fuerza débil actúa de manera universal sobre todos los leptones: electrones, muones, taus y sus neutrinos correspondientes.

En una dispersión por corriente neutra (mediada por $ Z^0 $), dos leptones interactúan intercambiando un bosón $Z^0$.

En este caso, las partículas no cambian de sabor, aunque redistribuyen su energía y momento.

Por ejemplo, un neutrino muónico puede dispersarse elásticamente en un electrón mediante el intercambio de un $Z^0$: $$ \nu_\mu + e^- \;\to\; \nu_\mu + e^- $$ Ambos conservan su identidad; solo cambian su energía y dirección.

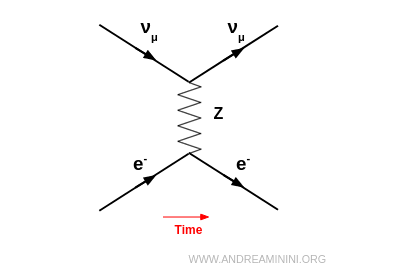
En una dispersión por corriente cargada (mediada por $W$), un leptón cargado y el neutrino de su misma generación se transforman entre sí (por ejemplo $ e^- \leftrightarrow \nu_e $, $ e^+ \leftrightarrow \bar{\nu}_e $) a través del intercambio de un $W$.

$$ l^- \leftrightarrow \nu_l + W^- $$

De este modo, en las interacciones débiles los leptones solo se convierten dentro de su propia familia.

• El electrón $(e^-)$ interactúa únicamente con su neutrino correspondiente $(\nu_e)$
• El muón $(\mu^-)$ lo hace con el neutrino muónico $(\nu_\mu)$
• El tau $(\tau^-)$ solo con el neutrino tauónico $(\nu_\tau)$

En todo vértice de Feynman se cumple estrictamente la conservación del número leptónico.

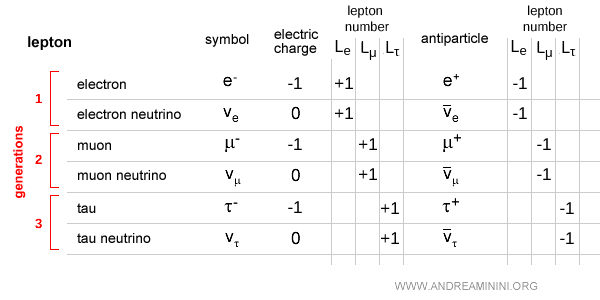
Explicación. En las interacciones débiles, cada leptón cargado se acopla únicamente con el neutrino de su propia generación a través del bosón $W$. Así, en un vértice débil de un diagrama de Feynman, los números leptónicos $L_e$, $L_\mu$ y $L_\tau$ se conservan de manera independiente. Dicho de otro modo: un electrón nunca puede transformarse en un neutrino muónico, ni un muón en un neutrino electrónico. En resumen, la fuerza débil conserva el número leptónico dentro de cada familia por separado.

La interacción puede describirse de forma equivalente como la emisión o la absorción de un bosón $W$.

Emisión de un bosón W

Cualquier leptón cargado puede emitir un bosón $W$:

• Un leptón negativo ($e^-$, $\mu^-$, $\tau^-$) puede transformarse en su neutrino emitiendo un $W^-$: $$ \ell^- \;\to\; \nu_\ell + W^- $$
• Un antileptón positivo ($e^+$, $\mu^+$, $\tau^+$) realiza la conversión inversa, pasando a su antineutrino mientras emite un $W^+$: $$ \ell^+ \;\to\; \bar{\nu}_\ell + W^+ $$

Así, los leptones negativos emiten $W^-$, mientras que sus antipartículas emiten $W^+$.

Por ejemplo, un muón negativo $\mu^-$ puede transformarse en un neutrino muónico $\nu_\mu$ emitiendo un $W^-$. Ese $W^-$ puede ser absorbido por un neutrino electrónico $\nu_e$, generando un electrón $e^-$: $$ \mu^- + \nu_e \;\to\; \nu_\mu + e^- $$

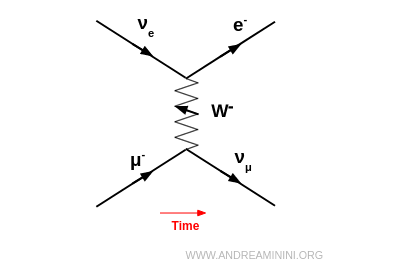
Si el $W^-$ emitido no es absorbido, puede desintegrarse en un electrón y un antineutrino electrónico: $$ W^- \;\to\; e^- + \bar{\nu}_e $$ En ese caso, el proceso global corresponde a la desintegración del muón: $$ \mu^- \;\to\; \nu_\mu + e^- + \bar{\nu}_e $$

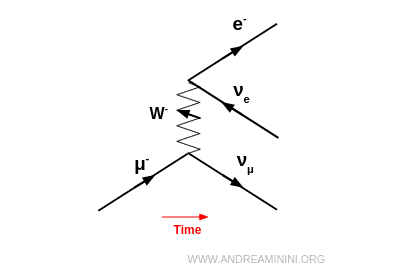
Absorción de un bosón W

A la inversa, los leptones pueden absorber un bosón $W$ y transformarse en su compañero correspondiente:

• Un neutrino puede absorber un $W^-$ y convertirse en el leptón cargado asociado: $$ \nu_\ell + W^- \;\to\; \ell^- $$
• Un antineutrino puede absorber un $W^+$ y transformarse en el leptón positivo correspondiente: $$ \bar{\nu}_\ell + W^+ \;\to\; \ell^+ $$

Por ejemplo, un positrón ($e^+$) puede transformarse en su antineutrino electrónico $\bar{\nu}_e$ emitiendo un $W^+$. Ese mismo $W^+$ puede ser absorbido por un antineutrino muónico $\bar{\nu}_\mu$, produciendo un muón positivo $\mu^+$. El proceso completo es: $$ e^+ + \bar{\nu}_\mu \;\to\; \bar{\nu}_e + \mu^+ $$

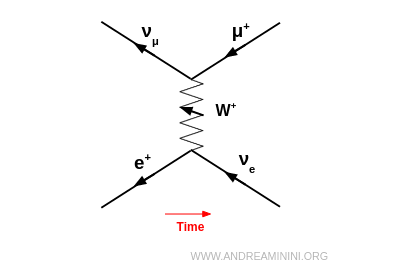
Al tratarse de antipartículas, sus flechas en el diagrama de Feynman se dibujan en sentido opuesto al flujo del tiempo, aunque el diagrama se interpreta de izquierda a derecha siguiendo el eje temporal físico.

Interacción débil entre quarks

La interacción débil cargada entre quarks, mediada por los bosones $W^\pm$, permite que un quark con carga $+\tfrac{2}{3}e$ se transforme en otro con carga $-\tfrac{1}{3}e$, o viceversa. Estas transiciones pueden darse no solo dentro de la misma generación, sino también entre generaciones distintas, con probabilidades determinadas por los elementos de la matriz CKM.

Por ejemplo, los quarks con carga $-\tfrac{1}{3}$ (down $d$, strange $s$, bottom $b$) pueden transformarse en quarks con carga $+\tfrac{2}{3}$ (up $u$, charm $c$, top $t$) mediante la emisión de un bosón $W^-$.

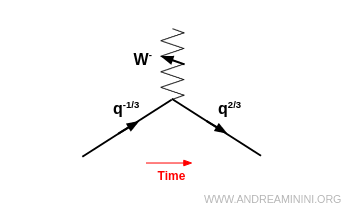
En este proceso, el quark conserva su número bariónico pero cambia de sabor.

Nota. El bosón $W^-$ no “se lleva” el sabor. Es el propio quark el que cambia de identidad durante la transición.

El bosón $W$ emitido puede:

• desintegrarse espontáneamente en un par leptón-antineutrino ($e^- + \bar\nu_e$, $\mu^- + \bar\nu_\mu$, etc.).
  

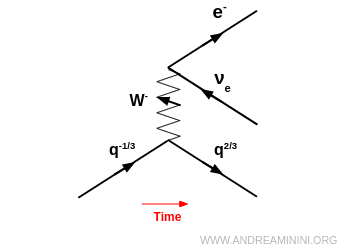
  Nota. Esto es exactamente lo que ocurre en la desintegración beta $β^-$, cuando un neutrón se convierte en un protón: $ n \to p + e^- + \bar{\nu}_e $
  

• ser absorbido por un neutrino, convirtiéndolo en el leptón cargado correspondiente (por ejemplo $ \nu_e \to e^- $). Esto conduce a un proceso semileptónico como $ d + \nu_e \to u + e^- $.
  
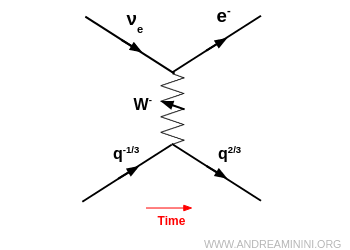
• ser absorbido por otro quark, provocando un cambio de sabor en un vértice débil distinto (proceso puramente hadrónico).

  Por ejemplo, la partícula $ \Lambda $ es un barión formado por tres quarks (up, down y strange), perteneciente a la familia de los hiperones. Se desintegra en un protón y un pión, $ \Lambda \to p + \pi^- $, mediante la conversión de un quark extraño (s) en un quark up (u).
  
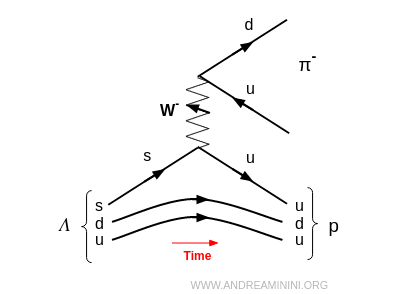
  Este caso ilustra un punto crucial: un quark strange (s) se transforma en un quark up (u), mostrando una transición entre diferentes generaciones de quarks.

Al principio, los físicos esperaban que los quarks, al igual que los leptones, obedecieran la regla de que los vértices débiles estaban restringidos a una sola generación. Para su sorpresa, descubrieron que los quarks pueden cambiar de sabor entre generaciones.

En 1963, Nicola Cabibbo propuso que los quarks tipo down ($d, s$) no participan en las interacciones débiles como estados “puros”, sino como combinaciones lineales. Introdujo así el ángulo de Cabibbo para explicar desintegraciones con cambio de extrañeza.

Una década después, en 1973, Makoto Kobayashi y Toshihide Maskawa extendieron este marco a tres generaciones de quarks.

De ahí surgió la matriz CKM (Cabibbo-Kobayashi-Maskawa), que describe cómo se mezclan las generaciones de quarks en las interacciones débiles, con los estados tipo down ($d,s,b$) apareciendo como combinaciones lineales.

En la práctica, el quark down $d$ no se acopla exclusivamente al $u$, sino a una mezcla de $d, s, b$. Lo mismo ocurre con $c$ y $t$.

$$ (u,d'),\quad (c,s'),\quad (t,b') $$

Aquí $d', s', b'$ son “quarks mezclados”, es decir, combinaciones lineales de $d, s, b$.

$$ d' = V_{ud}\, d + V_{us}\, s + V_{ub}\, b $$

$$ s' = V_{cd}\, d + V_{cs}\, s + V_{cb}\, b $$

$$ b' = V_{td}\, d + V_{ts}\, s + V_{tb}\, b $$

Por ejemplo, $V_{ud}$ indica cuánto contribuye el quark $d$ al estado $d'$, $V_{us}$ cuánto contribuye el $s$, y así sucesivamente.

De forma compacta, estas combinaciones lineales pueden escribirse como un producto vector-matriz: 

$$
\begin{pmatrix} d' \\ s' \\ b' \end{pmatrix}
=
\begin{pmatrix}
V_{ud} & V_{us} & V_{ub} \\
V_{cd} & V_{cs} & V_{cb} \\
V_{td} & V_{ts} & V_{tb}
\end{pmatrix}
\begin{pmatrix} d \\ s \\ b \end{pmatrix}
$$

Esta matriz de coeficientes $V_{ij}$ es lo que llamamos la matriz CKM (Cabibbo-Kobayashi-Maskawa).

Si fuese exactamente la matriz identidad, simplemente tendríamos $d'=d$, $s'=s$, $b'=b$.

Pero no lo es: aunque la matriz CKM se parece mucho a la identidad, no es idéntica.

Esto significa que los quarks pueden cambiar de sabor no solo dentro de su generación, sino también entre generaciones, cuando interactúan mediante la fuerza débil.

Nota. Sin este mecanismo, el quark $u$ solo podría convertirse en un $d$ y viceversa. Pero como $V_{us} \neq 0$, también puede transformarse en un quark strange $s$. Esto explica los procesos con cambio de extrañeza.

En resumen, la matriz CKM describe cómo los quarks tipo up ($u, c, t$) pueden transformarse en quarks tipo down ($d, s, b$) con probabilidades específicas.

La matriz CKM determinada experimentalmente (valores de 2020) muestra la magnitud de estas amplitudes de probabilidad:

$$ \begin{bmatrix} |V_{ud}| & |V_{us}| & |V_{ub}| \\ |V_{cd}| & |V_{cs}| & |V_{cb}| \\ |V_{td}| & |V_{ts}| & |V_{tb}| \end{bmatrix} = \begin{bmatrix} 0.97370 \pm 0.00014 & 0.2245 \pm 0.0008 & 0.00382 \pm 0.00024 \\ 0.221 \pm 0.004 & 0.987 \pm 0.011 & 0.0410 \pm 0.0014 \\ 0.0080 \pm 0.0003 & 0.0388 \pm 0.0011 & 1.013 \pm 0.030 \end{bmatrix} $$

De la primera fila, por ejemplo, vemos que el quark up ($u$) se acopla a un quark down ($d$) con una amplitud de alrededor del 97%, a un strange ($s$) con un 22%, y a un bottom ($b$) con apenas un 0.4%.

Nota. La suma $97% + 22% + 0.4%$ supera el 100% porque se trata de amplitudes, no de probabilidades. Las probabilidades reales se obtienen al elevar cada coeficiente al cuadrado: $$ |V_{ud}|^2 + |V_{us}|^2 + |V_{ub}|^2 = 1 $$ Para el ejemplo: $$ |V_{ud}|^2 \approx (0.974)^2 \approx 0.949 $$ $$ |V_{us}|^2 \approx (0.225)^2 \approx 0.051 $$ $$ |V_{ub}|^2 \approx (0.0038)^2 \approx 0.000014 $$ La suma da exactamente 1: $$ 0.949 + 0.051 + 0.000014 \approx 1.000. $$

Estos valores indican qué desintegraciones débiles son comunes y cuáles están suprimidas:

• $u \to d$ es la transición más probable, razón por la cual protones y neutrones constituyen la materia ordinaria.
• $s \to u$ es posible pero menos frecuente, y explica las desintegraciones extrañas ($\Lambda, \Sigma, \Omega$).
• $t \to b$ es prácticamente segura: el quark top casi siempre se desintegra en un quark bottom.

Así, un quark $u$ puede emitir un $W^+$ y convertirse en un $d$, pero también -aunque con menor probabilidad- en un $s$ o un $b$.

Nota. En los leptones, el vértice débil conecta siempre partículas de la misma generación, conservando los números leptónicos. La mezcla entre generaciones aparece solo más tarde, mediante las oscilaciones de neutrinos. En los quarks, en cambio, la mezcla entre generaciones está incorporada directamente en el vértice débil cargado y se describe con la matriz CKM. El principio es el mismo -el bosón $W$ media transiciones entre “up” y “down”- pero el emparejamiento ya no está restringido a una sola generación: la fuerza débil permite transiciones mixtas entre quarks de generaciones distintas.

Notas

Algunas observaciones adicionales sobre las interacciones débiles:

• Contribuciones débiles neutras dentro de procesos electromagnéticos
  En toda dispersión mediada por fotones (interacción electromagnética), existe en principio un diagrama análogo mediado por el bosón $Z^0$ (corriente débil neutra). A bajas energías, la contribución del $Z$ es despreciable frente al intercambio de fotones. Solo a energías muy altas -comparables a la masa del bosón $Z^0$ (unos $91$ GeV)- su efecto se vuelve significativo y medible.
  

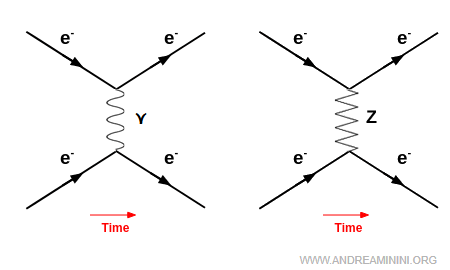
  Nota. Un ejemplo histórico proviene de la dispersión electrón-positrón de alta energía ($e^- + e^+ \to \mu^- + \mu^+$), estudiada en el DESY (Deutsches Elektronen-Synchrotron) en Hamburgo durante las décadas de 1970 y 1980, donde se observaron correcciones por intercambio de bosones neutros. Esto proporcionó evidencia experimental de efectos débiles incluso en procesos electromagnéticos: en la práctica, una ligera corrección a la ley de Coulomb, que desaparece a bajas energías. Para aislar una corriente neutra pura, libre de superposición electromagnética, la prueba más limpia es la dispersión de neutrinos, ya que los neutrinos no tienen carga y no acoplan a fotones. Sin embargo, estos experimentos son notoriamente complejos por la sección eficaz extremadamente pequeña de los neutrinos.

 Y así sucesivamente.