Matrice triangulaire inférieure
Une matrice carrée est dite triangulaire inférieure lorsque tous les éléments situés au-dessus de la diagonale principale sont nuls : $$ \forall \ i < j, \ \ \ a_{ij} = 0 $$
Exemple
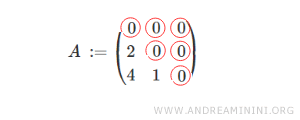
Considérons une matrice triangulaire inférieure d’ordre 3, c’est-à-dire composée de trois lignes et de trois colonnes.
On remarque que tous les coefficients placés au-dessus de la diagonale principale sont égaux à zéro.

Remarque : Les coefficients situés sur la diagonale, ainsi que ceux placés en dessous, ne sont soumis à aucune contrainte : ils peuvent être nuls ou non.
Si, en outre, tous les coefficients de la diagonale principale sont nuls, on parle alors d’une matrice strictement triangulaire inférieure.
L’ensemble des matrices triangulaires inférieures à coefficients réels et d’ordre \( n \) se note usuellement \( T_{R} \).
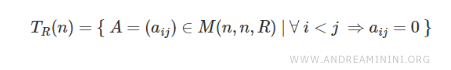
Remarque : Les matrices triangulaires présentent un intérêt pratique considérable, car l’information est concentrée dans une seule région de la matrice. Cela entraîne une diminution du nombre d’opérations arithmétiques nécessaires et une utilisation plus efficiente de la mémoire.
Intérêt des matrices triangulaires inférieures
Dans une matrice triangulaire inférieure, les coefficients non nuls se répartissent exclusivement dans la partie inférieure de la matrice. Cette structure favorise une représentation plus efficace de l’information, tant sur le plan du stockage que sur celui du calcul.
En outre, le déterminant d’une matrice triangulaire se calcule immédiatement comme le produit des coefficients de la diagonale principale, les autres termes n’ayant aucune incidence sur le résultat.
Et ainsi de suite…