Théorème du Sous-espace pour les Produits d’Espaces Topologiques

Soient $A$ et $B$ deux sous-ensembles respectifs des espaces topologiques $X$ et $Y$, $$ A \subset X $$ $$ B \subset Y $$ alors la topologie sur le produit $A \times B$, considérée comme sous-espace de $X \times Y$, coïncide avec la topologie produit sur $A \times B$ construite à partir des topologies induites sur $A$ et $B$ par $X$ et $Y$ : $$ \quad \tau_{A \times B}^{\text{sub}} = \tau_A^{\text{sub}} \times \tau_B^{\text{sub}} $$

Ici, $\tau_{A \times B}^{\text{sub}}$ désigne la topologie de sous-espace sur $A \times B$ induite par celle de $X \times Y$,

tandis que $\tau_A^{\text{sub}}$ et $\tau_B^{\text{sub}}$ sont les topologies de sous-espace sur $A$ et $B$, respectivement induites par $X$ et $Y$.

Ce théorème établit que les deux démarches conduisent à une topologie identique sur $A \times B$.

Autrement dit, la topologie obtenue en considérant $A \times B$ comme sous-espace de $X \times Y$ est rigoureusement la même que celle obtenue en formant le produit des topologies induites sur $A$ et $B$.

Quel que soit le point de départ choisi, on parvient à la même structure topologique sur $A \times B$.

Un Exemple Concret

Illustrons maintenant le théorème à l’aide d’un exemple explicite.

Considérons deux espaces topologiques $X$ et $Y$. Par exemple, prenons le plan cartésien, où $X$ correspond à l’axe des abscisses, et $Y$ à l’axe des ordonnées.

Soient $A \subseteq X$ et $B \subseteq Y$ deux sous-ensembles de ces espaces.

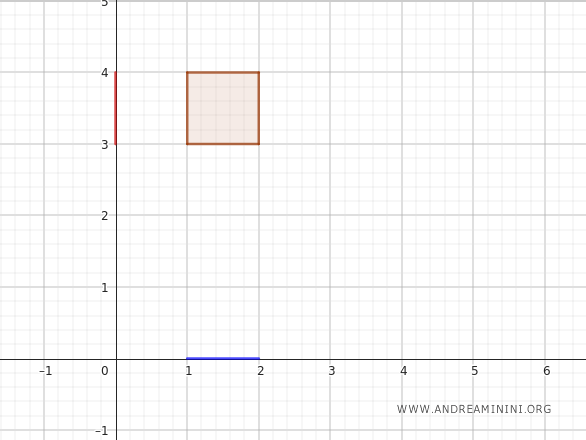
Par exemple, on peut prendre $A = [1, 2]$, un intervalle de l’axe des $x$, et $B = [3, 4]$, un intervalle de l’axe des $y$.

Le produit cartésien $A \times B$ est alors constitué de tous les couples $(x, y)$ tels que $x \in A$ et $y \in B$.

Ce produit décrit un rectangle du plan, dont les côtés sont parallèles aux axes, avec $x$ variant entre 1 et 2, et $y$ entre 3 et 4.

illustration du sous-espace

On peut définir une topologie sur $A \times B$ de deux manières :

Topologie de sous-espace
On considère $A \times B$ comme un sous-ensemble de $X \times Y$, c’est-à-dire du plan entier, muni de la topologie produit. La topologie sur $A \times B$ est alors celle induite par restriction de celle de $X \times Y$.
Topologie produit
Alternativement, on munit $A$ et $B$ des topologies qu’ils héritent respectivement de $X$ et $Y$, puis on construit la topologie produit sur $A \times B$ en tant que produit de ces topologies induites.

Ces deux constructions donnent exactement la même topologie sur $A \times B$.

Ainsi, quelle que soit la méthode adoptée, le résultat topologique final sur $A \times B$ reste inchangé.

Et ainsi de suite...