Interaction faible

L’interaction faible est l’une des forces fondamentales de la nature, aux côtés de l’interaction forte, de l’électromagnétisme et de la gravitation. Elle agit à la fois sur les leptons (électrons, neutrinos, etc.) et sur les quarks, et se manifeste par l’échange de bosons médiateurs : $W^+$, $W^-$ et $Z^0$. On parle parfois aussi de charge faible.

Il s’agit de la seule force capable de modifier la saveur des particules élémentaires, en transformant un quark ou un lepton en un autre de la même famille.

Cette propriété la rend responsable de processus tels que la désintégration bêta dans les noyaux instables. Comme les neutrinos sont produits et détectés via des interactions faibles dans leurs états de saveur, cette force est également au cœur du phénomène d’oscillations de neutrinos.

Son portée est extrêmement réduite (de l’ordre de $10^{-18}$ m), et son intensité est bien moindre que celle de l’interaction forte ou de l’électromagnétisme. À basse énergie, elle peut être jusqu’à $10^{11}$ fois plus faible que la force électromagnétique.

Il faut préciser que les valeurs données pour l’intensité relative des forces ne sont que des estimations valables aux basses énergies. En réalité, les constantes de couplage dépendent de l’échelle d’énergie considérée. Globalement, l’interaction faible est entre $10^{5}$ et $10^{13}$ fois plus faible que l’interaction forte.

Remarque. Malgré sa faiblesse, l’interaction faible joue un rôle essentiel, aussi bien en physique des particules qu’en astrophysique : c’est elle qui rend possibles les réactions nucléaires à l’origine de la lumière des étoiles.

Désintégration bêta et interaction faible

L’interaction faible est à l’origine de la désintégration bêta, un processus radioactif qui permet à un noyau atomique instable d’évoluer vers un état plus stable.

Un noyau est instable lorsqu’il présente un rapport déséquilibré entre neutrons et protons.

La désintégration bêta corrige ce déséquilibre en convertissant un neutron en proton, ou inversement. C’est l’une des principales formes de radioactivité naturelle, avec les désintégrations alpha et gamma.

• Désintégration bêta (β⁻)
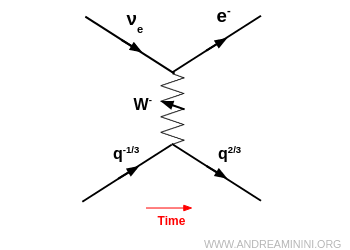
  Un neutron se transforme en proton en émettant un électron et un antineutrino électronique : $$ n \;\;\to\;\; p + e^- + \bar{\nu}_e $$ Au niveau des quarks, un quark down se convertit en quark up en émettant un boson virtuel \$W^-\$, lequel se désintègre quasi instantanément en \$e^-\$ et \$\bar{\nu}\_e\$.
  
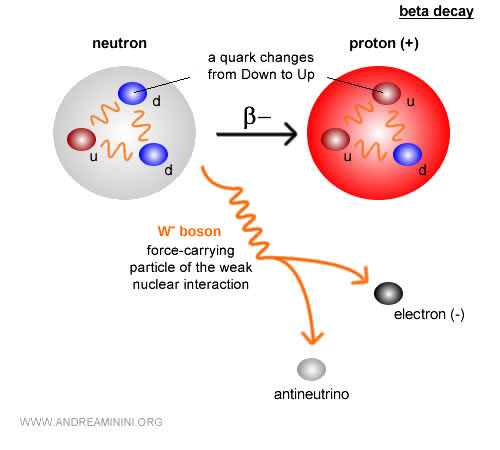
• Désintégration bêta (β⁺)
  Un proton se transforme en neutron en émettant un positron et un neutrino électronique : $$ p \;\;\to\;\; n + e^+ + \nu_e $$ Ici, un quark up se change en quark down en émettant un boson virtuel \$W^+\$, qui se désintègre ensuite en \$e^+\$ et \$\nu\_e\$.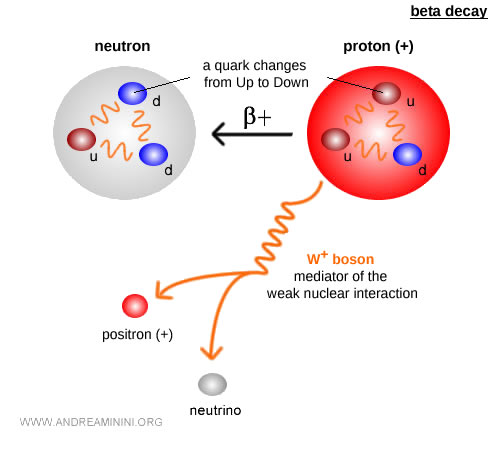

  

Ce mécanisme permet au noyau de rétablir un rapport neutrons/protons plus équilibré, atteignant ainsi une configuration énergétiquement plus stable.

Outre son rôle dans la radioactivité naturelle, la désintégration bêta intervient de manière cruciale dans les réactions nucléaires qui alimentent les étoiles, y compris le Soleil.

Modalités de l’interaction faible : neutre et chargée

L’interaction faible se présente sous deux formes distinctes.

• Interactions faibles neutres (NC, Neutral Current)
  Elles sont médiées par les bosons $Z$. Dans ce cas, le fermion qui entre dans le vertex est identique à celui qui en ressort : il n’y a pas de changement de saveur, comme dans les interactions électromagnétiques ou fortes. Leur signature spécifique est la violation de la parité, un marqueur qui permet de les identifier même lorsqu’elles restent masquées derrière des processus dominés par l’électromagnétisme, par exemple en physique atomique.

  Remarque. Les interactions chargées furent mises en évidence dès les années 1930 grâce aux travaux pionniers de Fermi sur la désintégration bêta. Les interactions neutres, en revanche, ne furent prédites qu’à la fin des années 1960 par Glashow, Weinberg et Salam, dans le cadre de la théorie électrofaible (GWS). Leur existence fut confirmée au CERN en 1973, constituant un jalon majeur de la physique des particules : jusque-là seuls les processus médiés par les bosons $W$ étaient connus, et la découverte des courants neutres marqua une véritable révolution.

• Interactions faibles chargées (CC, Charged Current)
  Elles sont médiées par les bosons $W$. Contrairement aux autres forces fondamentales, elles peuvent modifier la saveur des particules. Ainsi, un quark up peut devenir un quark down, ou un électron un neutrino électronique. Cette capacité à modifier la saveur fait des interactions chargées le moteur principal des processus de désintégration, tels que la désintégration bêta.

  Remarque. Dans l’interaction forte, les quarks peuvent changer de couleur (par exemple de rouge à vert) mais non de saveur ; dans l’interaction électromagnétique, les fermions (quarks et leptons) peuvent émettre ou absorber des photons sans altérer leur charge ni leur saveur. Il en va de même pour les interactions faibles neutres (NC), médiées par le boson $Z$. En revanche, dans les interactions faibles chargées (CC), médiées par les bosons $W^\pm$, une particule peut bel et bien changer de saveur : par exemple, un quark up peut se transformer en quark down, ce qui permet à un proton de devenir un neutron, ou inversement.

Avant d’examiner des cas concrets, le tableau suivant récapitule les différences essentielles entre interactions faibles neutres et chargées.

Type d’interaction	Médiateur	Changement de saveur	Caractéristique distinctive
Faible neutre (NC)	Boson Z0	Non	Viole la parité, mais conserve la charge et l’identité de la particule
Faible chargée (CC)	Bosons W±	Oui	Déclenche des processus de désintégration en transformant un fermion en un autre

Exemples pratiques

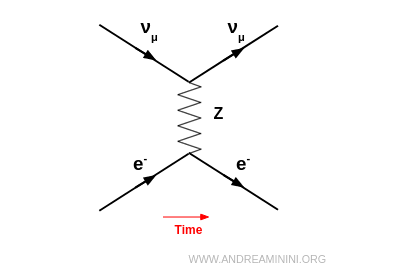
Parmi les manifestations classiques de l’interaction faible figurent la diffusion neutrino-électron $ \nu_{\mu} + e^- \to \nu_{\mu} + e^- $ et la diffusion neutrino-proton $ \nu_{\mu} + p \to \nu_{\mu} + p $.

Diffusion neutrino-électron

Dans ce processus, un neutrino ($\nu$) entre en collision avec un électron ($e^-$), le dévie et lui transfère une partie de son énergie et de sa quantité de mouvement : $$ \nu + e^- \;\to\; \nu + e^- $$ Un tel phénomène est extrêmement rare, les neutrinos n’ayant pas de charge électrique et n’interagissant pas par l’électromagnétisme. L’interaction faible est donc leur seul canal d’interaction.

Deux mécanismes sont possibles :

• Courant neutre (médié par $Z^0$)
  Il concerne toutes les saveurs de neutrinos ($\nu_e, \nu_\mu, \nu_\tau$). Le neutrino échange un boson virtuel $Z^0$ avec l’électron et conserve sa saveur : $$ \nu_\mu + e^- \;\to\; \nu_\mu + e^- $$ Seules l’énergie et la direction varient, la collision restant élastique.
  
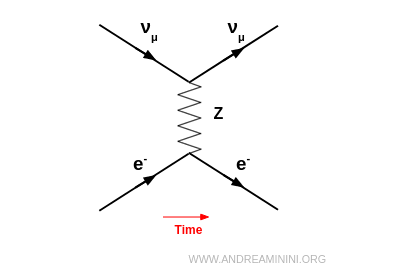
• Courant chargé (médié par $W^\pm$)
  Ici, un neutrino électronique $\nu_e$ se transforme en électron en échangeant un boson $W$ avec l’électron cible, lequel devient à son tour un neutrino électronique : $$ \nu_e + e^- \;\to\; e^- + \nu_e $$ En pratique, neutrino et électron échangent leur identité. Le résultat est analogue à la diffusion par courant neutre, mais le médiateur est cette fois un $W$ et non un $Z$.

Remarque. La diffusion neutrino-électron fut l’un des premiers processus à confirmer l’existence des courants neutres au CERN en 1973. On la qualifie de preuve « propre », car elle n’implique ni nucléons ni interaction forte, ce qui permet de tester directement la théorie électrofaible.

Diffusion neutrino-proton

Dans la diffusion neutrino-proton, le neutrino interagit directement avec un proton.

Dépourvus de charge électrique et insensibles à l’interaction forte, les neutrinos ne peuvent interagir que par l’échange de bosons faibles $W^\pm$ et $Z^0$.

Deux modalités principales existent, comme dans le cas neutrino-électron :

• Courant neutre (NC)
  Médié par le boson $Z^0$. Le neutrino conserve sa saveur et le proton reste inchangé. Seules l’énergie et la quantité de mouvement sont redistribuées (diffusion élastique). Exemple : $$ \nu_\mu + p \;\to\; \nu_\mu + p $$ Cette réaction joua un rôle clé dans la découverte des courants neutres au CERN en 1973.
  
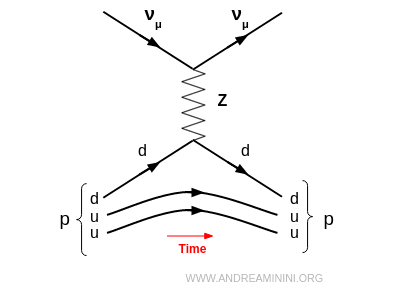
• Courant chargé (CC)
  Médié par un boson $W^\pm$. Le neutrino se convertit en lepton chargé tandis que le proton devient un autre nucléon (proton ↔ neutron). Ainsi, lorsqu’un neutrino électronique interagit avec un proton, il produit un positron et transforme le proton en neutron : $$ \nu_e + p \;\to\; e^+ + n $$ Ce processus constitue, en essence, l’inverse de la désintégration bêta.

Ces diffusions sont toutes deux d’une extrême rareté. Leur observation exige des détecteurs de grande taille et des faisceaux de neutrinos d’une intensité exceptionnelle.

Interaction faible entre leptons

L’interaction faible chargée entre leptons, médiée par les bosons $W^\pm$, permet à un neutrino (charge nulle) et à son lepton chargé associé (charge $-e$) de se transformer l’un en l’autre, mais toujours à l’intérieur de la même génération.

La force faible agit de manière universelle sur tous les leptons : électrons, muons, taus et leurs neutrinos respectifs.

Dans une diffusion par courant neutre (médiée par $Z^0$), deux leptons interagissent par l’échange d’un boson $Z^0$.

Les particules ne changent pas de saveur, mais réorganisent leur énergie et leur quantité de mouvement.

Exemple : un neutrino muonique peut se diffuser élastiquement sur un électron via l’échange d’un $Z^0$ : $$ \nu_\mu + e^- \;\to\; \nu_\mu + e^- $$ Les deux conservent leur identité ; seules l’énergie et la direction sont modifiées.

Dans une diffusion par courant chargé (médiée par $W$), un lepton chargé et le neutrino de sa propre génération se convertissent l’un en l’autre (par exemple $ e^- \leftrightarrow \nu_e $, $ e^+ \leftrightarrow \bar{\nu}_e $) par échange d’un boson $W$.

$$ l^- \leftrightarrow \nu_l + W^- $$

Ainsi, les transformations leptoniques induites par l’interaction faible restent strictement confinées à l’intérieur de chaque famille.

• L’électron $(e^-)$ n’interagit qu’avec son neutrino $(\nu_e)$
• Le muon $(\mu^-)$ uniquement avec le neutrino muonique $(\nu_\mu)$
• Le tau $(\tau^-)$ exclusivement avec le neutrino tauonique $(\nu_\tau)$

À chaque sommet de Feynman, la conservation du nombre leptonique est rigoureusement respectée.

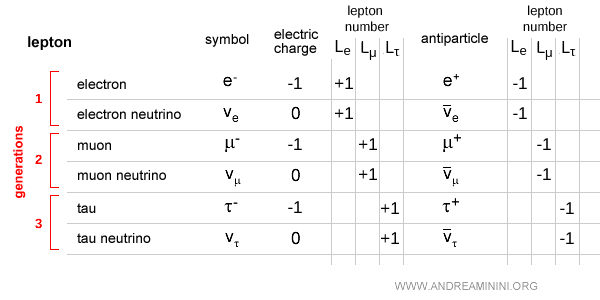
Explication. Dans les interactions faibles, chaque lepton chargé ne se couple qu’au neutrino de sa propre génération via un boson $W$. Ainsi, dans un sommet faible d’un diagramme de Feynman, les nombres leptoniques $L_e$, $L_\mu$ et $L_\tau$ se conservent séparément. Autrement dit, un électron ne peut jamais devenir un neutrino muonique, ni un muon un neutrino électronique. En résumé, la force faible conserve le nombre leptonique indépendamment dans chaque famille.

L’interaction peut aussi être décrite en termes d’émission ou d’absorption d’un boson $W$.

Émission d’un boson W

Tout lepton chargé peut émettre un boson $W$ :

• Un lepton négatif ($e^-$, $\mu^-$, $\tau^-$) peut se transformer en son neutrino en émettant un $W^-$ : $$ \ell^- \;\to\; \nu_\ell + W^- $$
• Un antilepton positif ($e^+$, $\mu^+$, $\tau^+$) effectue la conversion inverse, devenant son antineutrino tout en émettant un $W^+$ : $$ \ell^+ \;\to\; \bar{\nu}_\ell + W^+ $$

Ainsi, les leptons négatifs émettent des $W^-$, tandis que leurs antiparticules émettent des $W^+$.

Exemple : un muon négatif $\mu^-$ peut se transformer en neutrino muonique $\nu_\mu$ en émettant un $W^-$. Ce $W^-$ peut ensuite être absorbé par un neutrino électronique $\nu_e$, produisant un électron $e^-$ : $$ \mu^- + \nu_e \;\to\; \nu_\mu + e^- $$

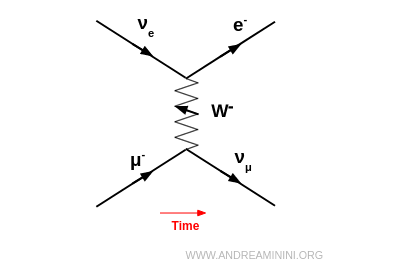
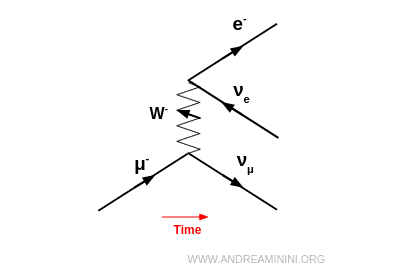
Si le $W^-$ émis n’est pas absorbé, il peut se désintégrer en un électron et un antineutrino électronique : $$ W^- \;\to\; e^- + \bar{\nu}_e $$ Le processus global correspond alors à la désintégration du muon : $$ \mu^- \;\to\; \nu_\mu + e^- + \bar{\nu}_e $$

Absorption d’un boson W

Inversement, les leptons peuvent absorber un boson $W$ et se transformer en leur partenaire associé :

• Un neutrino peut absorber un $W^-$ et devenir le lepton chargé correspondant : $$ \nu_\ell + W^- \;\to\; \ell^- $$
• Un antineutrino peut absorber un $W^+$ et se convertir en lepton positif associé : $$ \bar{\nu}_\ell + W^+ \;\to\; \ell^+ $$

Exemple : un positron ($e^+$) peut se transformer en son antineutrino électronique $\bar{\nu}_e$ en émettant un $W^+$. Ce $W^+$ peut ensuite être absorbé par un antineutrino muonique $\bar{\nu}_\mu$, produisant un muon positif $\mu^+$. Le processus complet est : $$ e^+ + \bar{\nu}_\mu \;\to\; \bar{\nu}_e + \mu^+ $$

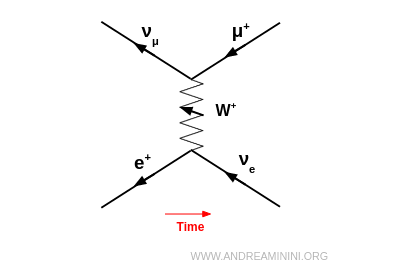
Comme il s’agit d’antiparticules, leurs flèches dans le diagramme de Feynman sont tracées en sens inverse du temps, mais le diagramme se lit toujours de gauche à droite selon l’axe temporel physique.

Interaction faible entre quarks

L’interaction faible chargée entre quarks, médiée par les bosons $W^\pm$, autorise la transformation d’un quark de charge $+\tfrac{2}{3}e$ en un quark de charge $-\tfrac{1}{3}e$, et inversement. Ces transitions ne se produisent pas seulement au sein d’une génération donnée, mais également entre générations différentes, avec des probabilités fixées par les éléments de la matrice CKM.

Concrètement, les quarks de charge $-\tfrac{1}{3}$ (down $d$, strange $s$, bottom $b$) peuvent se transformer en quarks de charge $+\tfrac{2}{3}$ (up $u$, charm $c$, top $t$) en émettant un boson $W^-$.

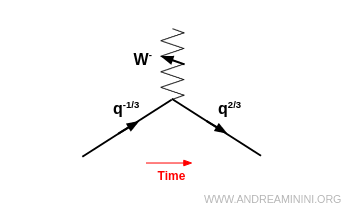
Lors de ce processus, le quark conserve son nombre baryonique mais change de saveur.

Remarque. Le boson $W^-$ ne « transporte » pas la saveur : c’est le quark lui-même qui change d’identité lors de la transition.

Le boson $W$ émis peut ensuite :

• se désintégrer spontanément en une paire lepton-antineutrino ($e^- + \bar\nu_e$, $\mu^- + \bar\nu_\mu$, etc.).
  

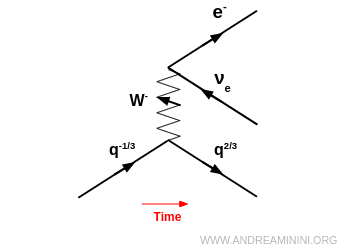
  Exemple. C’est exactement ce qui se produit dans la désintégration bêta $β^-$, lorsqu’un neutron se transforme en proton : $ n \to p + e^- + \bar{\nu}_e $
  

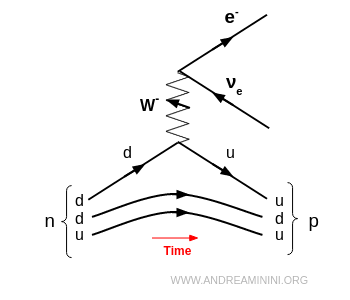
• être absorbé par un neutrino, qui devient alors le lepton chargé correspondant (par exemple $ \nu_e \to e^- $). On obtient ainsi un processus semi-leptonique du type $ d + \nu_e \to u + e^- $.
  
• être absorbé par un autre quark, provoquant un changement de saveur sur un second sommet faible (processus purement hadronique).

  Exemple : la particule $ \Lambda $, un baryon composé de trois quarks (up, down et strange) appartenant à la famille des hyperons, se désintègre en un proton et un pion, $ \Lambda \to p + \pi^- $, par conversion d’un quark strange (s) en quark up (u).
  
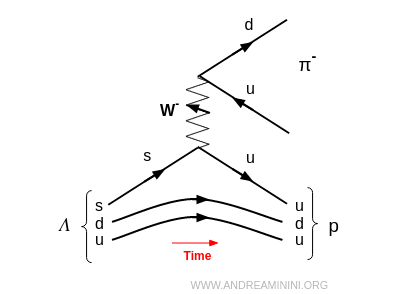
  Ce cas illustre un point clé : un quark strange (s) peut se transformer en quark up (u), révélant une transition entre différentes générations de quarks.

Au départ, on pensait que les quarks, comme les leptons, ne pouvaient interagir faiblement qu’au sein de leur propre génération. Or, l’expérience a montré qu’ils peuvent effectivement changer de saveur entre générations.

En 1963, Nicola Cabibbo proposa que les quarks de type down ($d, s$) n’interviennent pas dans les interactions faibles comme états « purs », mais comme combinaisons linéaires. Il introduisit l’angle de Cabibbo pour rendre compte des désintégrations avec changement d’étrangeté.

Dix ans plus tard, en 1973, Makoto Kobayashi et Toshihide Maskawa généralisèrent ce schéma à trois générations de quarks.

C’est ainsi qu’apparut la matrice CKM (Cabibbo-Kobayashi-Maskawa), qui décrit le mélange des générations de quarks dans les interactions faibles, les états de type down ($d, s, b$) apparaissant comme superpositions linéaires.

En pratique, un quark down $d$ ne se couple pas exclusivement au $u$, mais à une combinaison de $u, c, t$. Le même principe vaut pour $s$ et $b$.

$$ (u,d'),\quad (c,s'),\quad (t,b') $$

Ici, $d', s', b'$ désignent des « quarks mélangés », c’est-à-dire des superpositions linéaires de $d, s, b$.

$$ d' = V_{ud}\, d + V_{us}\, s + V_{ub}\, b $$

$$ s' = V_{cd}\, d + V_{cs}\, s + V_{cb}\, b $$

$$ b' = V_{td}\, d + V_{ts}\, s + V_{tb}\, b $$

Ainsi, $V_{ud}$ mesure la contribution du quark $d$ à l’état $d'$, $V_{us}$ celle du $s$, etc.

De manière compacte, ces relations se résument par un produit vecteur-matrice :

$$
\begin{pmatrix} d' \\ s' \\ b' \end{pmatrix}
=
\begin{pmatrix}
V_{ud} & V_{us} & V_{ub} \\
V_{cd} & V_{cs} & V_{cb} \\
V_{td} & V_{ts} & V_{tb}
\end{pmatrix}
\begin{pmatrix} d \\ s \\ b \end{pmatrix}
$$

Si cette matrice $V_{ij}$ était exactement l’matrice identité, on aurait simplement $d'=d$, $s'=s$, $b'=b$.

Mais ce n’est pas le cas : bien qu’elle soit très proche de l’identité, la matrice CKM présente de légères différences essentielles.

Résultat : les quarks peuvent changer de saveur non seulement à l’intérieur d’une génération, mais aussi d’une génération à l’autre, sous l’effet de l’interaction faible.

Remarque. Sans ce mécanisme, le quark $u$ ne pourrait se transformer qu’en $d$. Mais comme $V_{us} \neq 0$, il peut également se convertir en quark strange $s$. Cela explique l’existence des processus avec changement d’étrangeté.

En résumé, la matrice CKM décrit comment les quarks de type up ($u, c, t$) peuvent se transformer en quarks de type down ($d, s, b$) avec des probabilités bien déterminées.

La matrice CKM mesurée expérimentalement (valeurs de 2020) donne l’ordre de grandeur de ces amplitudes :

$$ \begin{bmatrix} |V_{ud}| & |V_{us}| & |V_{ub}| \\ |V_{cd}| & |V_{cs}| & |V_{cb}| \\ |V_{td}| & |V_{ts}| & |V_{tb}| \end{bmatrix} = \begin{bmatrix} 0.97370 \pm 0.00014 & 0.2245 \pm 0.0008 & 0.00382 \pm 0.00024 \\ 0.221 \pm 0.004 & 0.987 \pm 0.011 & 0.0410 \pm 0.0014 \\ 0.0080 \pm 0.0003 & 0.0388 \pm 0.0011 & 1.013 \pm 0.030 \end{bmatrix} $$

La première ligne, par exemple, montre que le quark up ($u$) se couple au quark down ($d$) avec une amplitude d’environ 97 %, au strange ($s$) avec 22 %, et au bottom ($b$) avec à peine 0,4 %.

Remarque. La somme $97\% + 22\% + 0,4\%$ excède 100 % car il s’agit d’amplitudes et non de probabilités. Celles-ci s’obtiennent en élevant chaque coefficient au carré : $$ |V_{ud}|^2 + |V_{us}|^2 + |V_{ub}|^2 = 1 $$ Exemple : $$ |V_{ud}|^2 \approx (0.974)^2 \approx 0.949 $$ $$ |V_{us}|^2 \approx (0.225)^2 \approx 0.051 $$ $$ |V_{ub}|^2 \approx (0.0038)^2 \approx 0.000014 $$ La somme vaut bien 1 : $$ 0.949 + 0.051 + 0.000014 \approx 1.000. $$

Ces valeurs indiquent quelles désintégrations faibles sont courantes et lesquelles sont fortement supprimées :

• $u \to d$ est la transition la plus probable, ce qui explique pourquoi protons et neutrons constituent la matière ordinaire.
• $s \to u$ est possible mais plus rare, et rend compte des désintégrations étranges ($\Lambda, \Sigma, \Omega$).
• $t \to b$ est pratiquement certaine : le quark top se désintègre presque toujours en quark bottom.

Ainsi, un quark $u$ peut émettre un $W^+$ et devenir un $d$, mais aussi - quoique bien moins fréquemment - un $s$ ou un $b$.

Remarque. Chez les leptons, le sommet faible relie toujours des particules d’une même génération, assurant la conservation des nombres leptoniques. Le mélange entre générations n’apparaît que plus tard, via les oscillations de neutrinos. Chez les quarks, en revanche, ce mélange intergénérationnel est intégré dès le sommet faible chargé et décrit par la matrice CKM. Le principe reste le même - le boson $W$ relie états « up » et « down » - mais l’appariement n’est plus limité à une seule génération : l’interaction faible autorise directement des transitions mixtes entre quarks de générations différentes.

Notes

Quelques remarques complémentaires sur les interactions faibles :

• Contributions faibles neutres aux processus électromagnétiques
  Dans toute diffusion médiée par des photons (interaction électromagnétique), il existe en principe un diagramme analogue médié par le boson $Z^0$ (courant neutre faible). À basse énergie, la contribution du $Z$ est négligeable devant l’échange de photons. Ce n’est qu’à des énergies proches de la masse du boson $Z^0$ (environ $91$ GeV) que son effet devient significatif.
  

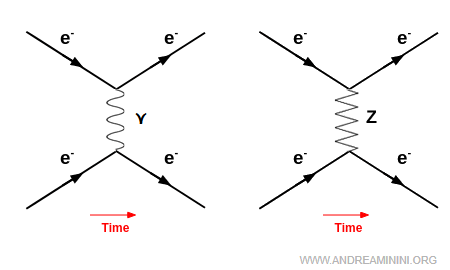
  Exemple historique. La diffusion électron-positron à haute énergie ($e^- + e^+ \to \mu^- + \mu^+$), étudiée au DESY (Deutsches Elektronen-Synchrotron) à Hambourg dans les années 1970-1980, mit en évidence des corrections dues à l’échange de bosons neutres. Cela fournit une preuve expérimentale d’effets faibles jusque dans des processus électromagnétiques : en pratique, une correction ténue à la loi de Coulomb, qui disparaît aux basses énergies. Pour isoler un courant neutre « pur », sans contribution électromagnétique, l’essai le plus probant reste la diffusion de neutrinos, car ceux-ci n’ont pas de charge et n’interagissent pas avec les photons. Mais de telles expériences sont d’une difficulté extrême, en raison de la section efficace extrêmement réduite des neutrinos.

 Et ainsi de suite.