Punto
En geometría euclidiana, un punto es una de las ideas básicas a partir de las cuales se construyen las rectas y los planos.

Se considera un concepto primitivo porque no se define a partir de otros. En geometría, algunos elementos simplemente se aceptan como fundamentales, y el punto es uno de ellos.
De forma intuitiva, entendemos un punto como algo sin dimensiones: no tiene longitud, anchura ni altura. Tampoco tiene forma ni partes. Euclides lo resumía diciendo que un punto es “aquello que no tiene partes”.
Cuando lo representamos sobre el papel, usamos una pequeña marca para indicar su posición. Esta marca no es el punto en sí, sino una aproximación visual necesaria para trabajar sobre un dibujo.
El símbolo que trazamos tiene tamaño y ocupa espacio, mientras que el punto, como concepto geométrico, es completamente adimensional. Cada vez que dibujamos un punto, en realidad estamos creando una representación física que nos ayuda a visualizar una idea abstracta.

En los textos de geometría, los puntos se nombran con letras mayúsculas, como \( A \), \( B \) o \( C \). Sirven para señalar de manera precisa una posición en el espacio.
En un plano cartesiano, un punto se describe mediante un par ordenado de coordenadas \((x, y)\). Estas dos cifras bastan para localizarlo exactamente.
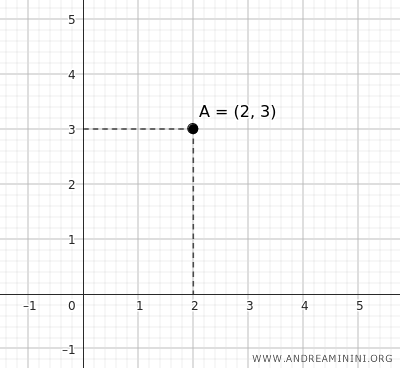
Por ejemplo, el punto A con coordenadas (2,3) está situado a 2 unidades del origen sobre el eje x y a 3 unidades sobre el eje y.
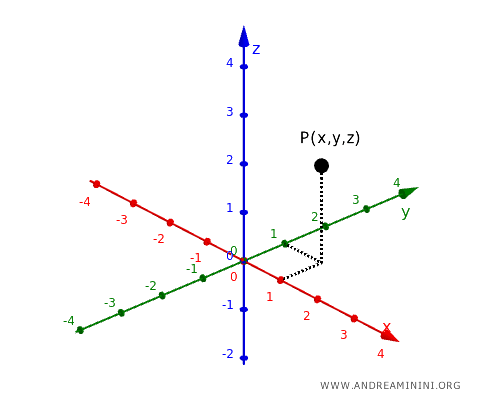
En el espacio tridimensional, la posición de un punto se determina con tres números: \((x, y, z)\). Cada uno indica su distancia respecto de los tres planos coordenados.
A partir del concepto de punto se construyen muchos otros elementos esenciales de la geometría clásica.
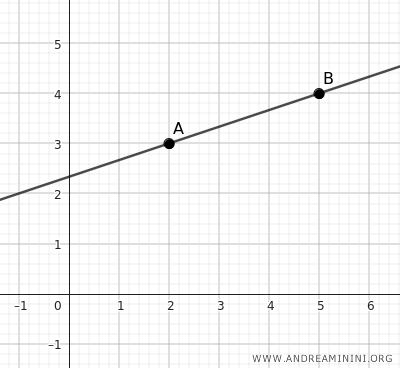
Por ejemplo, una recta queda determinada por dos puntos distintos. Podemos imaginarla como una sucesión infinita de puntos alineados en una misma dirección.
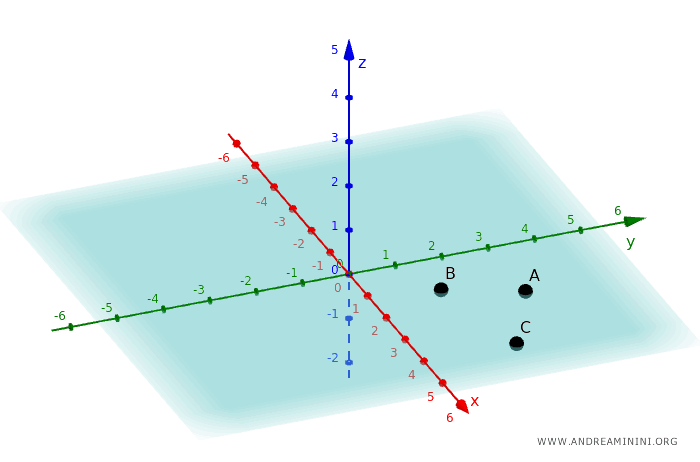
De manera similar, un plano queda fijado por tres puntos no colineales. Es una superficie plana de dos dimensiones formada por un número infinito de puntos.
Los puntos también son el punto de partida para construir segmentos, ángulos, polígonos y muchas otras figuras que aparecen constantemente en la geometría.