Ángulo Recto
Un ángulo recto es aquel que mide exactamente 90 grados, o π dividido entre dos radianes (π/2 rad).
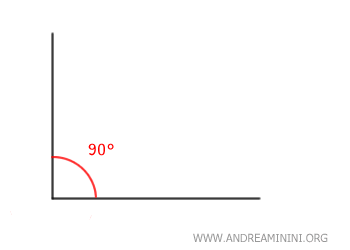
Es uno de los ángulos más fundamentales en geometría y suele representarse mediante un pequeño cuadrado en el vértice.
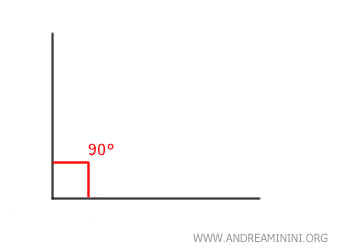
Un ángulo recto se forma cuando dos rectas se cruzan de manera perpendicular.
Equivale a la mitad (1/2) de un ángulo llano (180°) y a un cuarto (1/4) de una vuelta completa (360°).
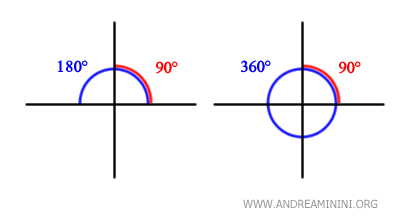
Se trata de un concepto esencial en numerosas ramas de las matemáticas, la ciencia y la ingeniería.
Por ejemplo, en arquitectura e ingeniería, la perpendicularidad es crucial para garantizar la estabilidad de edificios y estructuras. En matemáticas, los ángulos rectos son fundamentales en disciplinas como la trigonometría y la geometría euclidiana. En física, los ángulos rectos se utilizan con frecuencia en problemas de vectores, donde descomponer un vector en componentes perpendiculares facilita enormemente el análisis.
Aspectos Clave sobre los Ángulos Rectos
El ángulo recto posee varias propiedades únicas que lo convierten en un elemento indispensable en muchos campos de las matemáticas y la física.
Entre sus características más relevantes destacan:
- Dos rectas perpendiculares forman cuatro ángulos rectos.
Cuando dos rectas se cruzan formando un ángulo de 90 grados, se dice que son perpendiculares y generan cuatro ángulos rectos.
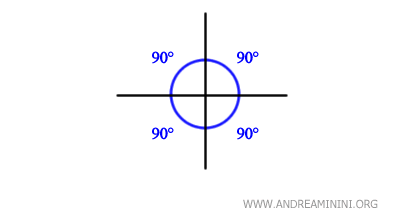
Esto se observa claramente en figuras geométricas como el cuadrado o el rectángulo, donde siempre se pueden identificar cuatro ángulos rectos.
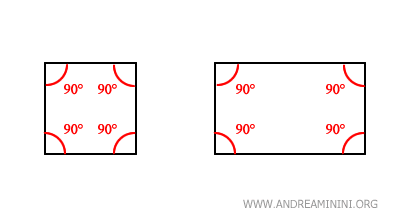
- Ángulos Complementarios
Se denominan “ángulos complementarios” aquellos dos ángulos cuya suma equivale a un ángulo recto.
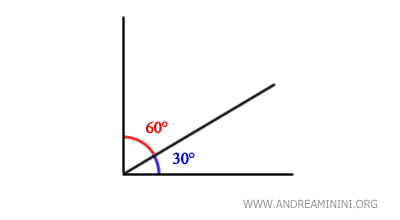
- Perpendicularidad
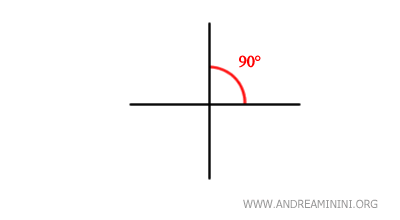
Dos rectas son perpendiculares si forman un ángulo recto en el punto donde se intersectan. Esta propiedad es clave en la geometría euclidiana.
- Triángulo Rectángulo
En un triángulo rectángulo, el ángulo recto es el ángulo opuesto al lado más largo, conocido como hipotenusa. - Teorema de Pitágoras
El teorema de Pitágoras establece que, en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. Es una de las relaciones más fundamentales en matemáticas.
Historia
El ángulo recto es conocido desde la antigüedad.
Los antiguos egipcios utilizaban cuerdas con nudos para formar el llamado “triángulo egipcio” de lados 3, 4 y 5, un clásico ejemplo de triángulo rectángulo. Empleaban este método para trazar ángulos rectos en sus construcciones.
Los números 3, 4 y 5 conforman también lo que se conoce como una “terna pitagórica”.
Más adelante, los antiguos griegos, especialmente Euclides, desarrollaron un sistema de geometría conocido como geometría euclidiana, en el cual el ángulo recto desempeña un papel central.
Por ejemplo, el teorema de Pitágoras es uno de los principios matemáticos más célebres desarrollados por los griegos de la Antigüedad y está directamente relacionado con los triángulos rectángulos, que contienen un ángulo recto.
Y así sucesivamente.